Indulging in the beautiful field called multi-robot path planning using Private Obstacle Path Planning algorithm
So first let me lay the groundwork for what the problem is? And why and what I am trying to achieve here. Let's start with why the hell I need to do all this?
Any sufficiently advanced technology is indistinguishable from magic.
- Arthur C. Clarke
Why?
So this was a brainchild of the trying to replicate delivery of packages to multiple places using any number of robots. Hence this raised the need to be able to plan in multiagent fashion.
What was I trying to achieve?
So my aim in the team was to come up with a planning method which will be able to coordinate between all the different robots such that they don't collide. Now this needs to happen keeping in mind that overall performance of the robot should be maximized.
Solving this problem can be divided into 2 broad categories: coupled approach and decoupled approach. This division is broadly based on the computational requirement and optimality of the solution generated by the method. In multi-agent problems one needs to achieve optimal balance between achieving computational complexity and optimality of the solution.
For this reason I wished to go with the decoupled approach. It’s way less taxing on the computation side and should give an optimized path.
Defining the Problem Statement
The following was how the arena on which testing was done looked like. The black regions are obstacles and the small notches made at (1,5) and (1,10) are the starting positions. The white area is where the robots can move around. The goals (9 in total) are given in the middle of map as a group of 4 black boxes.
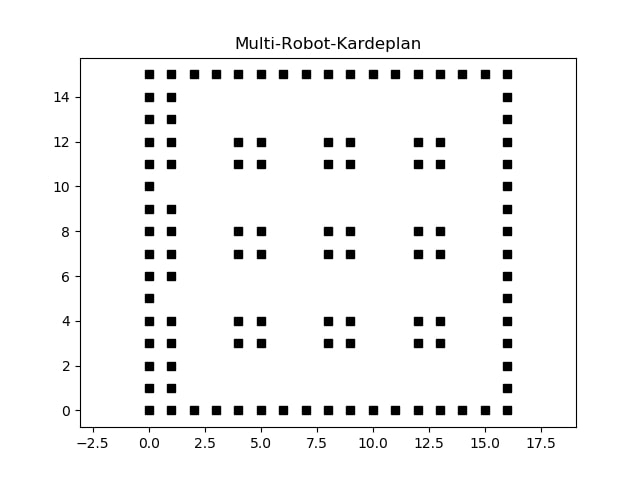
For this problem statment, I had to make the following assumptions:
- Related to Agent - Start and goal configuration for each agent is clearly defined. - They move at constant speeds. - Their trajectory is followed closely with small error. - Related to Environment - Environment (or the workspace) is fully observable. - Environment is a discrete space, which the agent can move only at fixed units of distance. - Related to Execution - It’s a centralized execution system - Execution is done using a frame based system.
Previous Work
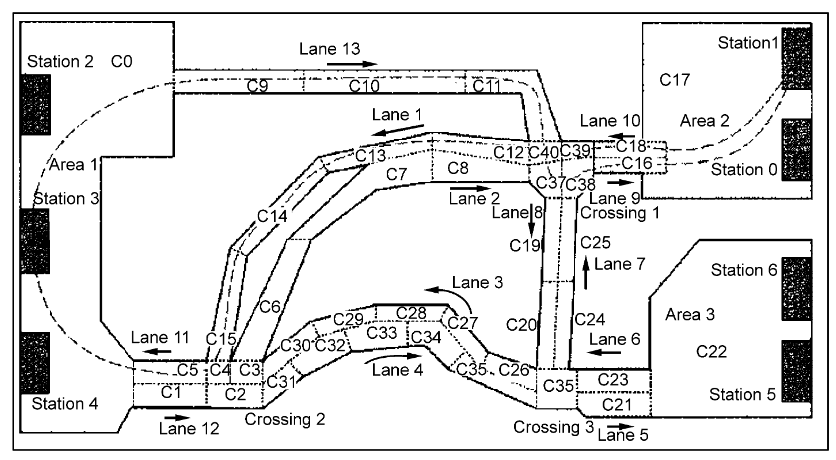
Among the highly cited papers I found was one stuck out for the simplicity and the beauty, “A Distributed and Optimal Motion Planning Approach for Multiple Mobile Robots” written by Guo and Parke, 2002 [1]. They talk about an approach of using coordination diagrams to do collision checks and then maximize the performance attribute of all the robots by varying the velocity profile of the robots. This approach is quite straightforward but in the scenario I tried it in there were quite a lot of times the robots ended up in deadlock as it was not changing the path of the robots.
.png)
Going into more detail we can define the solution, where each agent Ri
charts a path
$$\tau:[0,1] \xrightarrow{} R_{s,free}^i $$
Coordination diagram is used to optimize the velocity of each agent,
$$ X = [0,1]^m $$
coordination diagram for m robots. When agent is at 0 its considered to be at its starting position and when it reaches 1, it has reached the goal. The objective can be then defined to reach to
$$ h(0,1) \xrightarrow{} X_{free} $$
where $$ X_{free}= X - X_{obs} $$
Based on the above explanation we can define global performance index to be:
$$
\tau = \beta_1\times max(T_1,T_2,...Tm) + \beta_2\times \sum_{i=1}^m T_{idleTime,i} $$
where, Ti denotes time spent by each of the m agents to reach the goal, IidleTime,i denotes idle time for the robots and β1, β2 are the weights.
To solve this problem one use D* velocity planning, where the cost function would something like:
$$
f_v = \eta + \alpha_1d+\alpha_2t_{idleTime} + \alpha_3p
$$
where η is some large value tending to ∞, tidleTime is the total idle time for all the m agents, d is euclidean distance from current position to the goal point, p is the penalty incurred when the agent has to stop and let other agent pass.
Private Obsctacle Planning
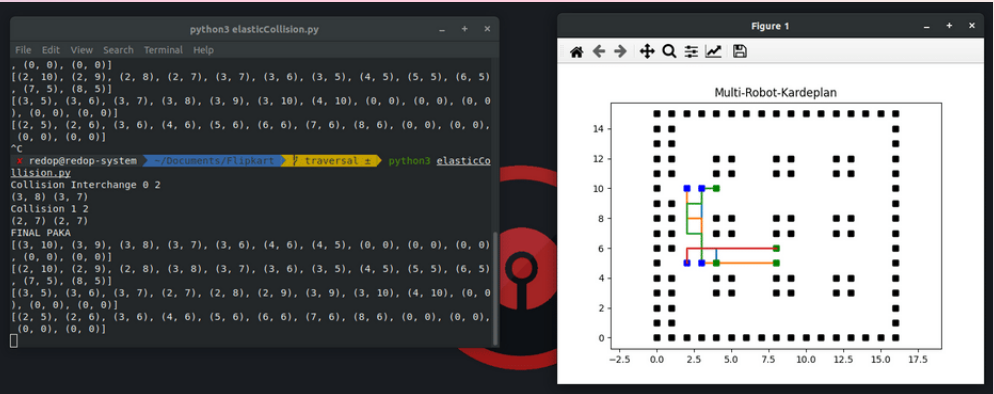
In this method instead of trying to manipulate the velocity of the agents such that they don't collide, we try to change their paths. First each agent plans its path towards their goal locations independent of other robots. Then collision detection and interchange detection is done for each pair of robots. Collision detection can be defined as when R1 is moving from (x1,y1) to a common location (xc,yc) while R2 is also moving from (x2,y2) to the common location then its defined as collision. Interchange detection is the case when R1 is going (x1,y1) → (x2,y2), but R2
is also going (x2,y2) → (x1,y1) even though they aren't at the same position at a singular point but this will also lead to a collision. This can also be thought of as a subset of the Collision detection where they collide at (x1.5,y1.5) considering R1 R2 are moving at constant speed. But as our assumption was that we have a discrete space we cant define x1.5 hence the need to define Interchange detection.
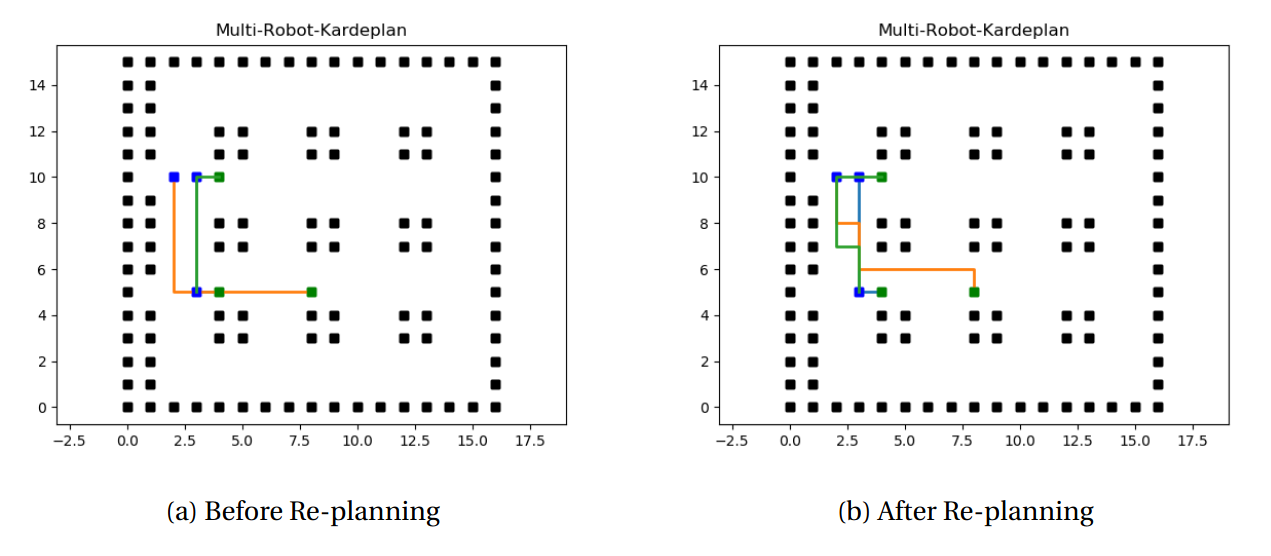
Once collisions are detected in accordance to priority order between different agents R1,...,Rm we need to define private obstacles ωi which is are obstacles, local and private to Ri agent. ωi depends on the priority order and collisions taking place between each agent Ri.
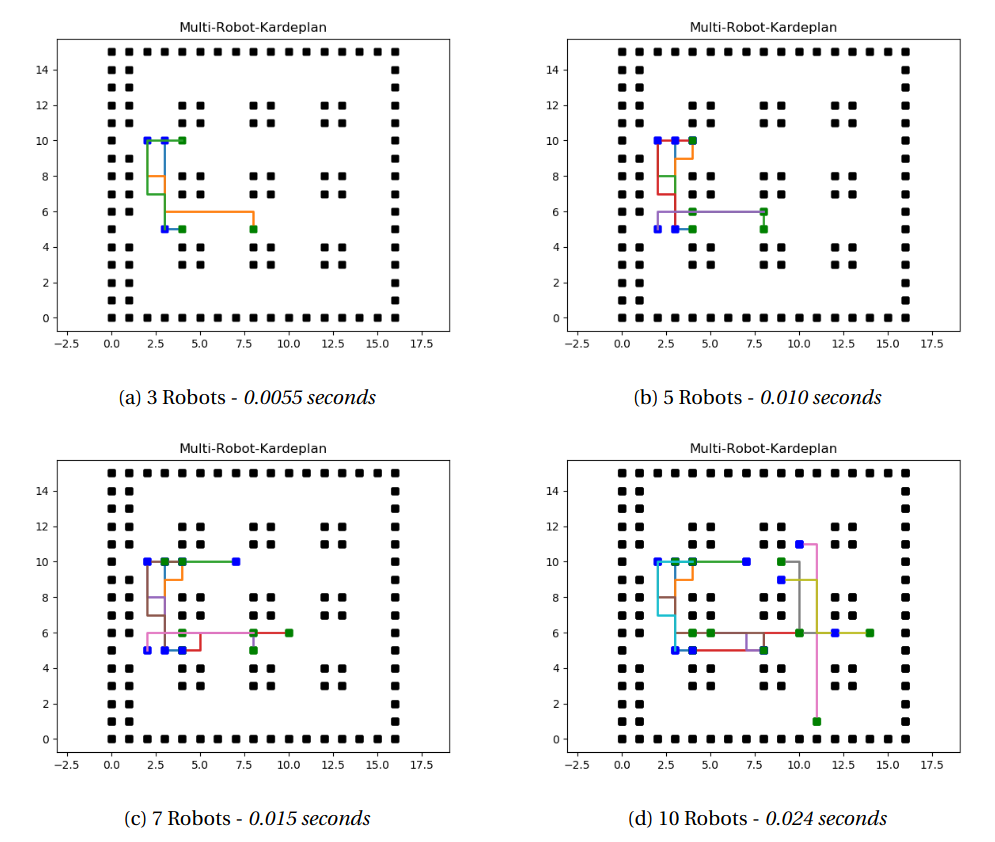
The time complexity of this problem is O(rn3), r is number of time slices, $n$ is number of edges in the system. From this we can observe it is faster method than Coupled Path Planing as it's reducing a high dimensional problem into one with much lower dimensional space. The only disadvantage with this method is that it doesn't consider the possibility of reducing speed or stopping agents at various time instants, hence the solution found might not be the most optimum one.
Future Work
To further optimize the algorithm one can use randomize search technique (hill climbing) to evaluate the best possible priority order for a set of agents. Going into detail how one can do this is by first starting off with initial priority order scheme selected in such a way that the agent with the longest path is given higher priority, one with the shortest path is given the least priority. Then priority order is exchanged between two agents in the scheme. If the new scheme results in a solution with shorter overall path of the agents than the best one found so far, it continues with this new order. Since hill-climbing has local min-mima problem, algorithm performs random restarts with different initial orders of the agents to minimize this issue to the least this thus defines, another cycle of trial. Like this we will have maxCycles denoting how many of these cycles it need to perform before selecting the best solution between them. We also define maxJumps to limit the max time spent on each cycle.
Up Next
In future I want to talk about how the algorithum is exactly working and try to quantize the results with different style and sized arena. Once the project is done will put all the documentation in the project section of the website.
Also fun-fact you can subscribe to the blog using RSS! For Firefox users you can use Livemark for this.
$ press CTRL+W to end the session.
[1] Yi Guo and L. E. Parker, "A distributed and optimal motion planning approach for multiple mobile robots," Proceedings 2002 IEEE International Conference on Robotics and Automation (Cat. No.02CH37292), 2002, pp. 2612-2619 vol.3, doi: 10.1109/ROBOT.2002.1013625.
[2] Lumelsky V.J., Harinarayan K.R. (1997) Decentralized Motion Planning for Multiple Mobile Robots: The Cocktail Party Model. In: Arkin R.C., Bekey G.A. (eds) Robot Colonies. Springer, Boston, MA. doi: 10.1007/978-1-4757-6451-2_7
[3] Parker L.E. (2009) Multiple Mobile Robot Teams, Path Planning and Motion Coordination in. In: Meyers R. (eds) Encyclopedia of Complexity and Systems Science. Springer, New York, NY. doi: 10.1007/978-0-387-30440-3_344