This is an innovative version of an angle, scale and position invariant template matching algorithm.
The goal was to create a template matching algorithm that can run in sub-200ms and is position, scale, and rotation invariant. The built-in template matching function of OpenCV is robust but only if you have positional invariance requirement. It fails if the object in the live footage rotates with respect to the master image.
Another algorithm explored was feature-matching. This ticked all the boxes. It is positional, rotational, and scale-invariant. But the challenge here was that it depends heavily on the individual blobs of the master image.
As you can see in the following image:
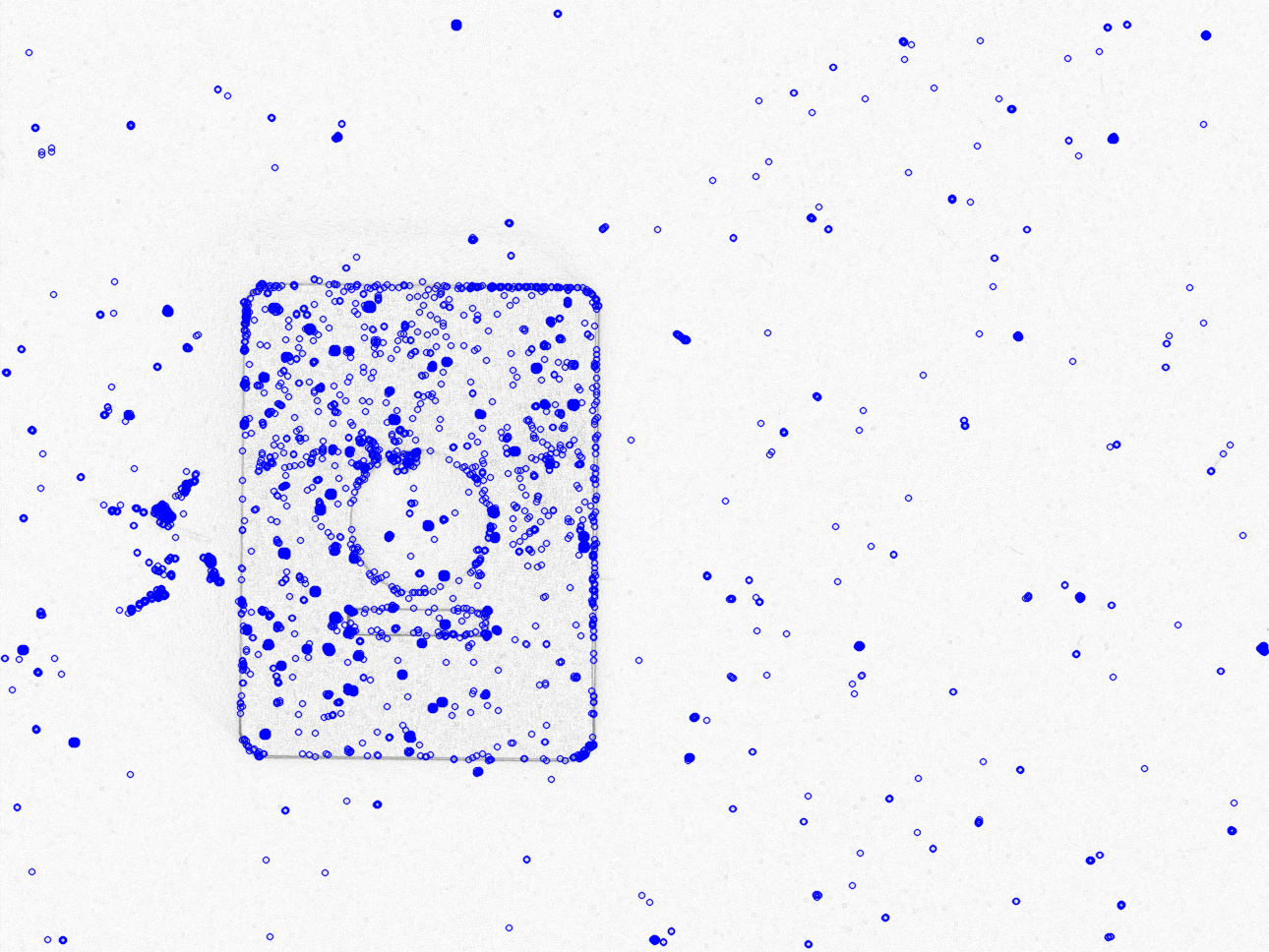
It picks up the features on the object which are too reliant on having that exact object shown to the system again. This is certainly improbable, and just having an extra scratch on the object will make the system reject it. Hence this may work in simulations but for real-life dataset, this can't be used.
Hence, I end up with FFT based template matching technique. For this, I used these papers as my basis [1], [2].
The architecture discussed in the papers had a higher runtime so it had to be optimized. I took only the bare bones of the architecture explained in the paper and applying filters and calculations which were less intensive. Allowing the algorithm to reach the set parameter.

Let's look at the technique:
The main tool leveraged in this method is FFT's time shift property -
$$ f_2 \lparen t \rparen = f_1 \lparen t-t_0 \rparen F_2 \lparen t \rparen = e^{-j\omega t_0}F_1 \lparen t \rparen $$
But instead of time shift we will use it to calculate shift in x and y axis.
$$ f_2 \lparen x,y \rparen = f_1(x-x_0,y-y_0) \newline F_2(\xi,\eta) = e^{-j2\pi(\xi x_0+\eta y_0)}F_1(\xi,\eta) $$
Now imagine consider F1 and F2 to be two images. So now when we take cross-power spectrum of the two images we get,
$$
\frac{F_1(\xi,\eta)F_2^*(\xi,\eta)}{|F_1(\xi,\eta)F_2(\xi,\eta)|} = e^{j2\pi(\xi x_0+\eta y_0)}
$$
Hence we can get the change in location as a power of e. But considering our target is to first find the angle, we need to convert the image from Cartesian plane to Polar plane. But even that won't be enough as the change in angle will be coming as a power of e. Thus, we need to take log-polar transform of the image. One more point to note is that even though we want just the rotation to be detected. But as we are going to apply this algorithm in real life it is possibile that the scale of the image also changes. This is due to distortion of lens and a number of other factors. Hence, we technically need to see the scale and rotation of the image.
Considering just rotation and translation for now,
$$ f_2 \lparen x,y \rparen = f_1\lparen x \cos{\theta_0} + y \sin{\theta_0} -x_0, -x \sin{\theta_0} + y \cos{\theta_0} -y_0 \rparen \newline F_2\lparen x,y \rparen = e^{-j2\pi(\xi x_0+\eta y_0)}F_1 \lparen \xi \cos{\theta_0} + \eta \sin{\theta_0}, -\xi\sin{\theta_0} + \eta \cos{\theta_0}\rparen $$
Taking Magnitude both sides,
$$ M_2(x\xi,\eta) = M_1(\xi \cos{\theta_0} + \eta \sin{\theta_0}, -\xi\sin{\theta_0} + \eta \cos{\theta_0}) $$
Hence we can write it as,
$$ M_1(\rho,\theta) = M_2(\rho,\theta - \theta_0) $$
Hence the angle can we found. Taking into account the scaling property of Fourier Transform,
$$ f_2 = f_1(ax,by)\newline F_2(\xi,\eta) = \frac{1}{|ab|}F_1(\xi/a,\eta/b) $$
So, for a rotated and scaled image we can write,
$$ M_1(\rho,\theta) = M_2(\rho/a,\theta-\theta_0) $$
Taking log both sides
$$ M_1(\log \rho,\theta) = M_2(\log \rho - \log a,\theta-\theta_0) $$
Using, $$ \xi = \log \rho \enspace \text{and} \enspace d = \log a $$
$$ M_1(\xi,\theta) = M_2(\xi - d,\theta-\theta_0) $$
Now, we can get both angle and scale by which the live image correlates to the master image. Now working off the angle value we rotate our template image and then use the OpenCV built-in template matching function working off coefficient score. This will provide us with the location of the object and then the data is sent to the Camera Setup.

Algorithm
Here, I am just giving you a brief of the whole algorithm and major steps involved in it. Readers are encouraged to read more about it by themselves through research papers.
Filter
Due to changes in lighting for our setup, we had to add a filter to keep the exposure almost similar throughout the day.

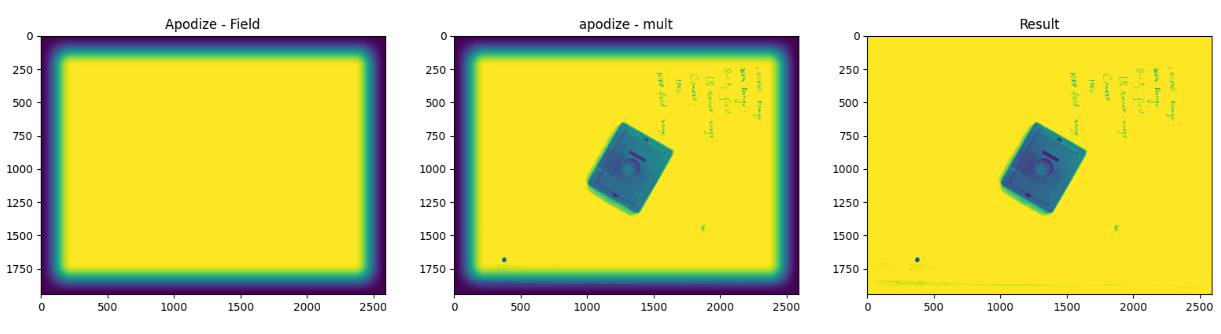
Apodization
The algorithm is basically to smooth out the border of the image to get rid of the tail noise in an image signal. Something like this,
DFT of the Image
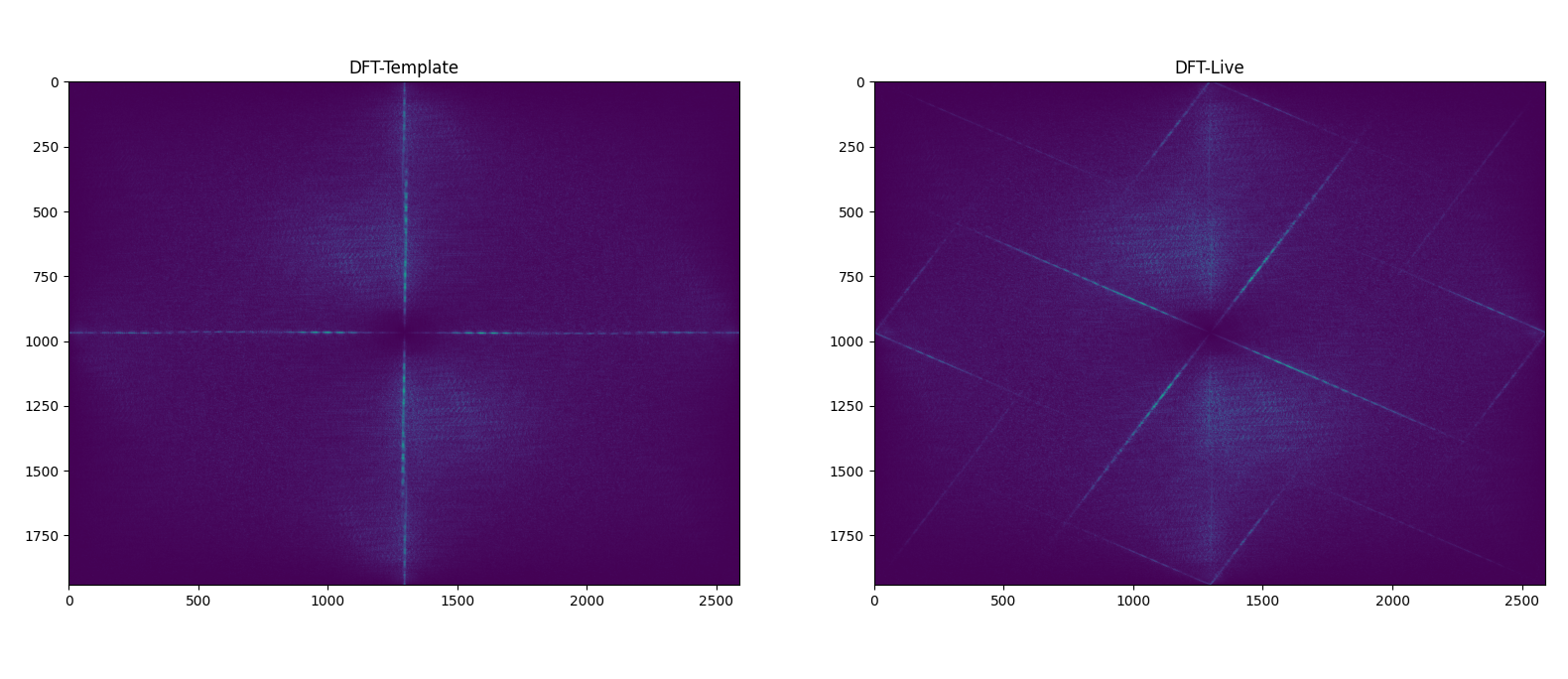
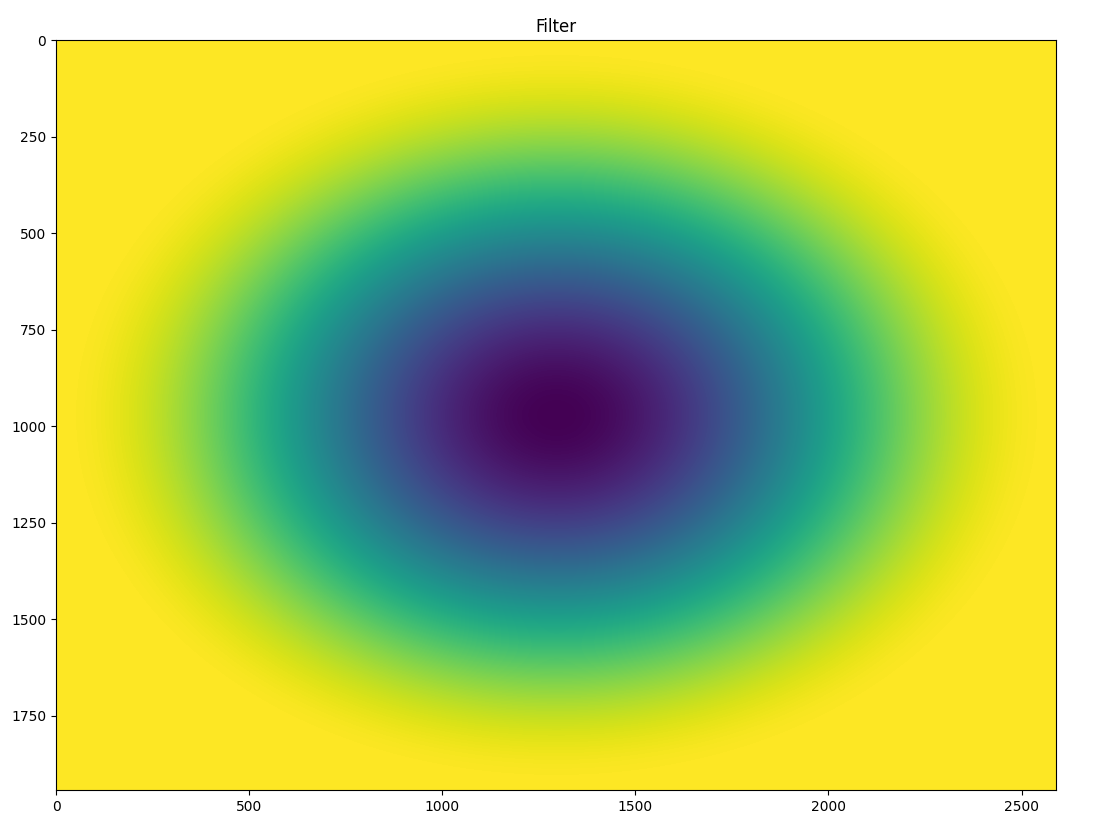
Applying High Pass filter in Polar Coordinates
The yellow region means 1.0 and the purple region means 0.0
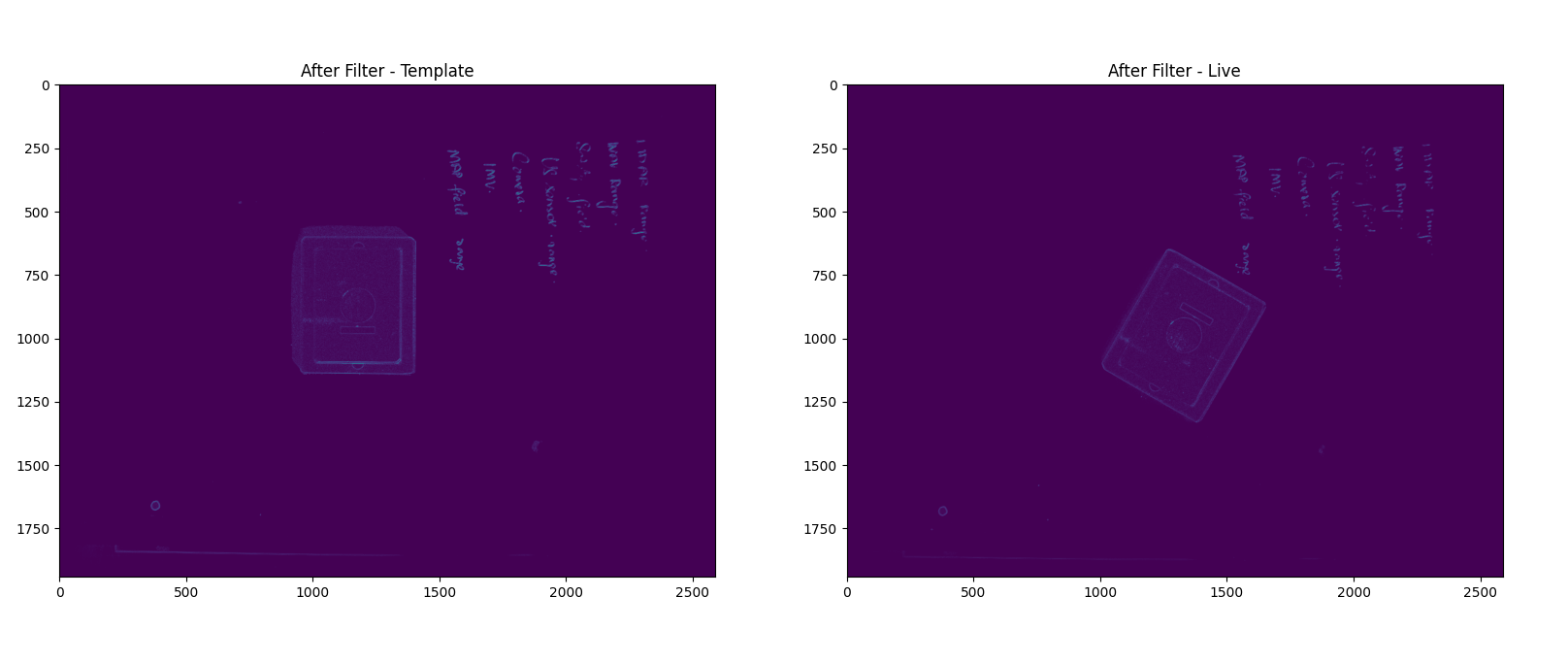
After applying it to the image this is what you get,
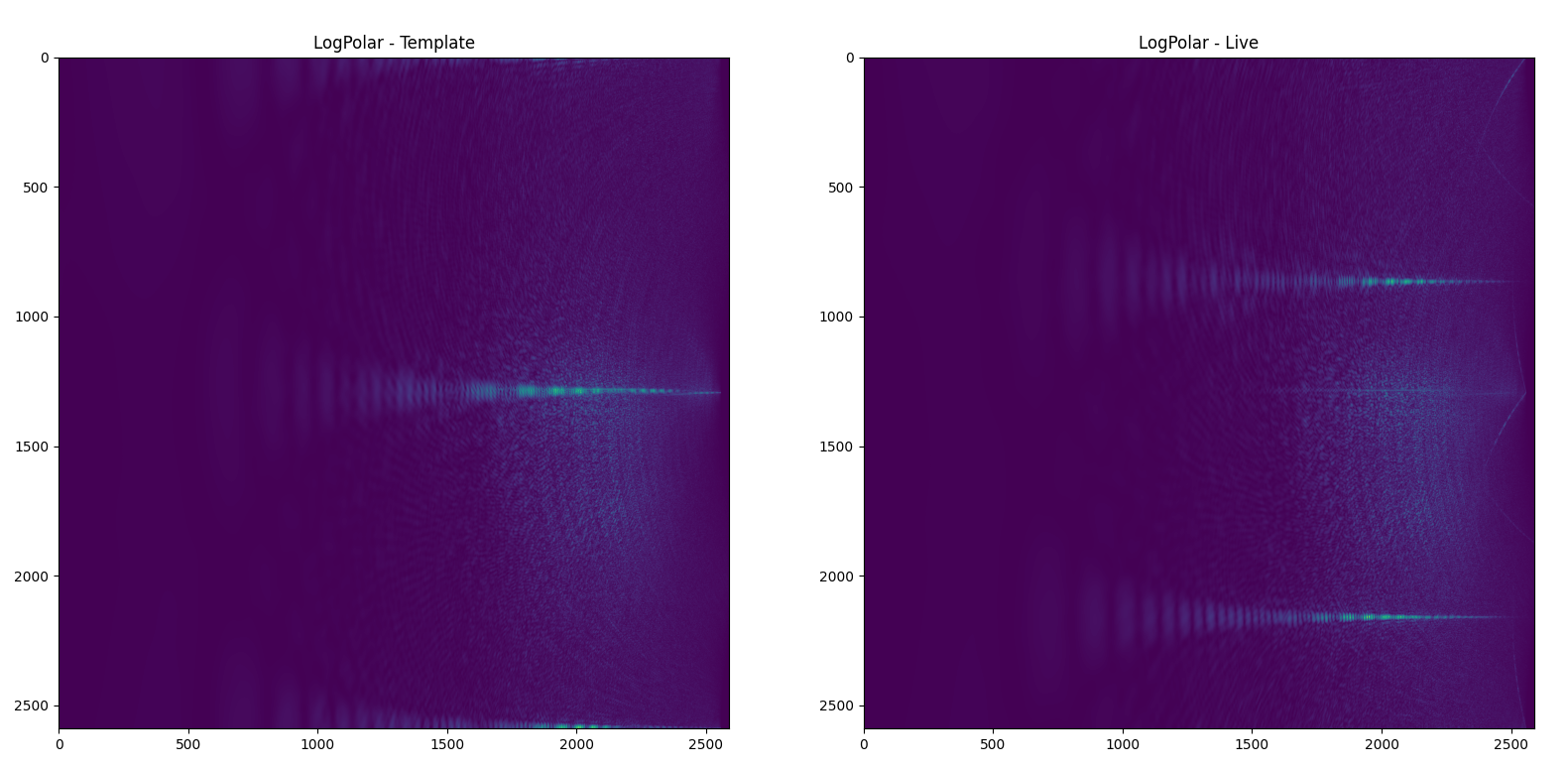
Log-Polar Conversion
As mentioned in the Algorithm section instead of just Polar-Transformation we actually need log-polar transform.
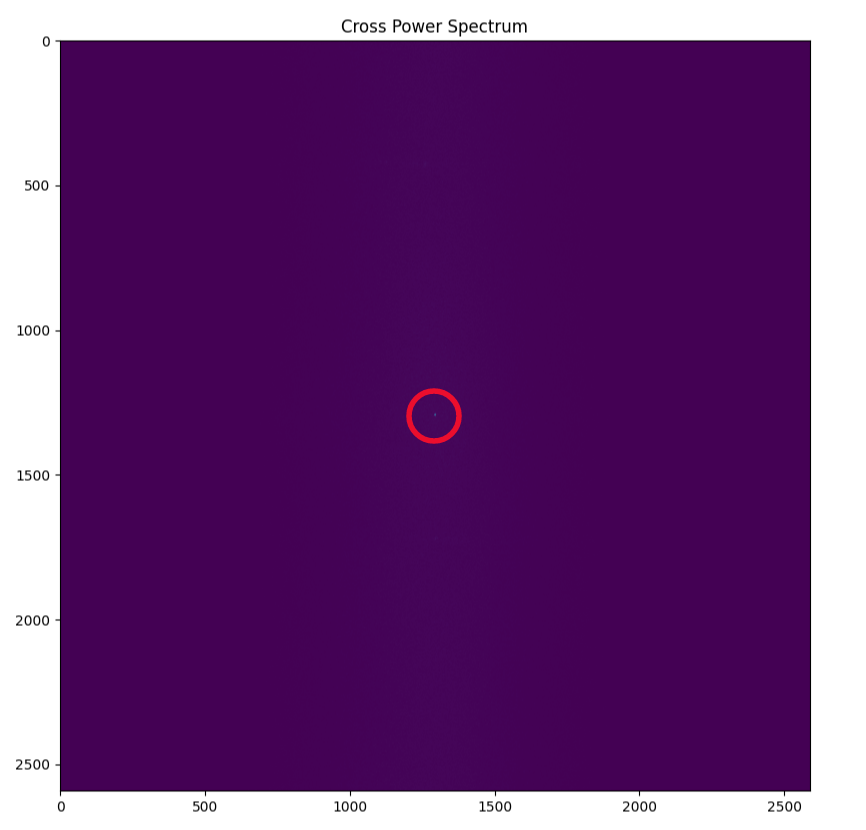
Cross-Power Spectrum of the Images
You can notice a small dot almost in the centre of the image. That dot is a unit function denoting the angle and scale with which the live image has changed as compared to the template.
Conclusion
This is part of a bigger project I worked on. After I talk about other parts of this project, I will post the codes and explain you how to test it on your system. So stay tuned over the blog section. Once everything is explained here I will post the guide on the projects section of the website. Also fun-fact you can subscribe to the blog using RSS! For Firefox users you can use Livemark for this.
$ press CTRL+W to end the session.
[1] Huy Tho Ho and R. Goecke, "Optical flow estimation using Fourier Mellin Transform," 2008 IEEE Conference on Computer Vision and Pattern Recognition, 2008, pp. 1-8, doi: 10.1109/CVPR.2008.4587553.
[2] B. S. Reddy and B. N. Chatterji, "An FFT-based technique for translation, rotation, and scale-invariant image registration," in IEEE Transactions on Image Processing, vol. 5, no. 8, pp. 1266-1271, Aug. 1996, doi: 10.1109/83.506761.